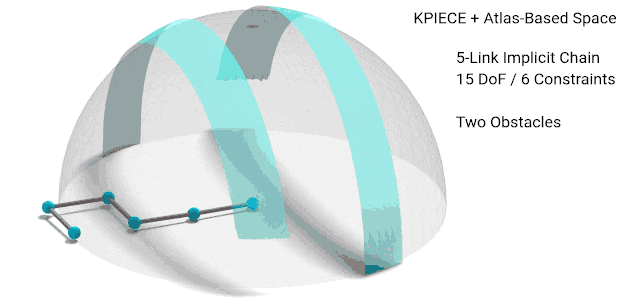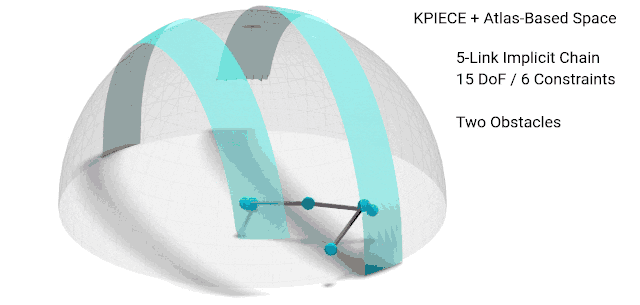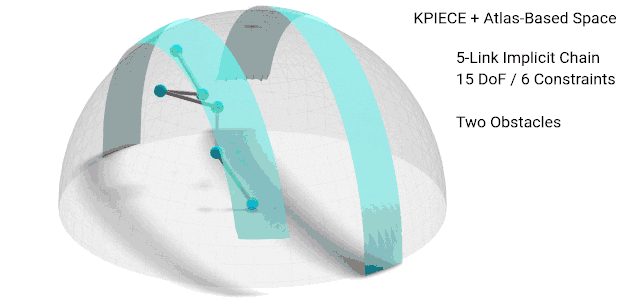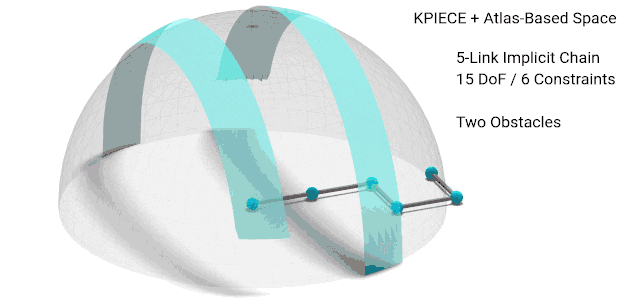
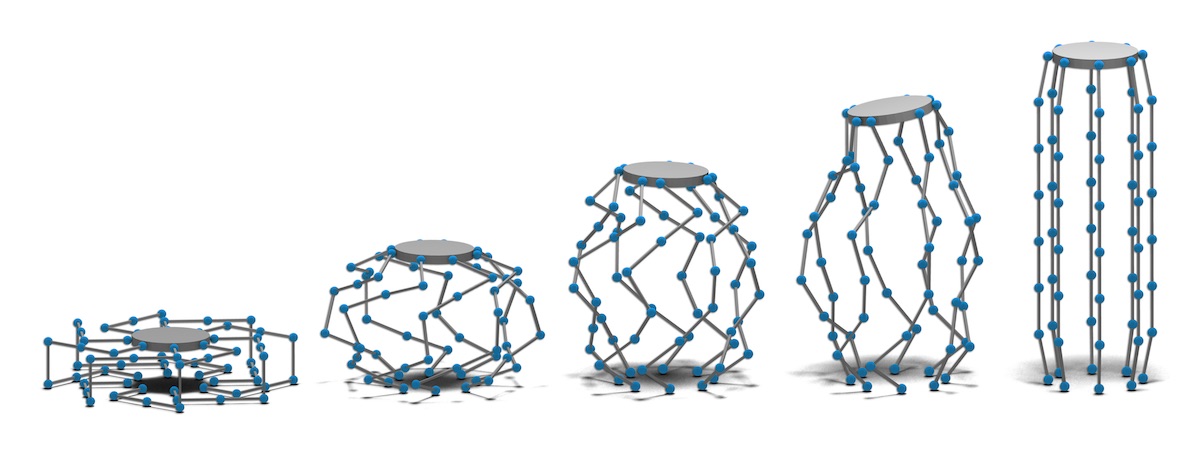
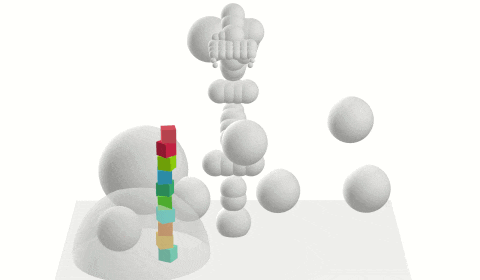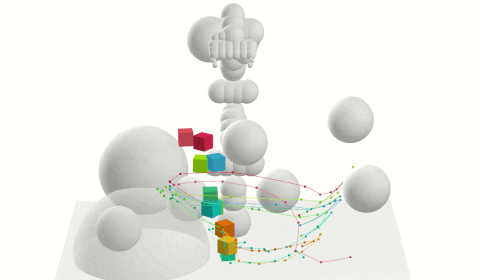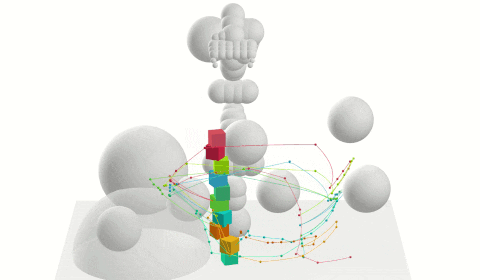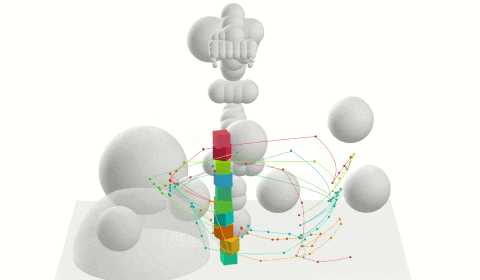Planning with Constraints
Interacting with the world imposes constraints on your motion: you open doors about their hinge, pull drawers along their rails, keep glasses of liquid upright so they do not spill, and more. Respecting these constraints while still generating feasible or optimal motion is complex and requires careful consideration in the design of planning algorithms and how the constraints are specified and satisfied. There are also many exciting considerations when there are many constraints that need to be satisfied simultaneously (e.g., a humanoid robot that must open a door, keep a glass upright, and maintain balance, or as shown in the video, a parallel mechanism with many interacting arms) or in sequence (e.g., as shown in the video, Robonaut 2 traversing multiple handrails, opening the hatch, and so on).
2025
- arXiv
Differentiable Particle Optimization for Fast Sequential ManipulationUnder ReviewSequential robot manipulation tasks require finding collision-free trajectories that satisfy geometric constraints across multiple object interactions in potentially high-dimensional configuration spaces. Solving these problems in real-time and at large scales has remained out of reach due to computational requirements. Recently, GPU-based acceleration has shown promising results, but prior methods achieve limited performance due to CPU-GPU data transfer overhead and complex logic that prevents full hardware utilization. To this end, we present SPaSM (Sampling Particle optimization for Sequential Manipulation), a fully GPU-parallelized framework that compiles constraint evaluation, sampling, and gradient-based optimization into optimized CUDA kernels for end-to-end trajectory optimization without CPU coordination. The method consists of a two-stage particle optimization strategy: first solving placement constraints through massively parallel sampling, then lifting solutions to full trajectory optimization in joint space. Unlike hierarchical approaches, SPaSM jointly optimizes object placements and robot trajectories to handle scenarios where motion feasibility constrains placement options. Experimental evaluation on challenging benchmarks demonstrates solution times in the realm of milliseconds with a 100% success rate; a 4000x speedup compared to existing approaches.
@misc{chen2025spasm, title = {Differentiable Particle Optimization for Fast Sequential Manipulation}, author = {Chen, Lucas and Iyer, Shrutheesh R. and Kingston, Zachary}, eprint = {2510.07674}, archiveprefix = {arXiv}, primaryclass = {cs.RO}, year = {2025}, note = {Under Review}, } - arXiv
Look as You Leap: Planning Simultaneous Motion and Perception for High-DoF RobotsQingxi Meng, Emiliano Flores, Carlos Quintero-Peña, Peizhu Qian, Zachary Kingston, Shannan K. Hamlin, Vaibhav Unhelkar, and Lydia E. KavrakiUnder ReviewIn this work, we address the problem of planning robot motions for a high-degree-of-freedom (DoF) robot that effectively achieves a given perception task while the robot and the perception target move in a dynamic environment. Achieving navigation and perception tasks simultaneously is challenging, as these objectives often impose conflicting requirements. Existing methods that compute motion under perception constraints fail to account for obstacles, are designed for low-DoF robots, or rely on simplified models of perception. Furthermore, in dynamic real-world environments, robots must replan and react quickly to changes and directly evaluating the quality of perception (e.g., object detection confidence) is often expensive or infeasible at runtime. This problem is especially important in human-centered environments such as homes and hospitals, where effective perception is essential for safe and reliable operation. To address these challenges, we propose a GPU-parallelized perception-score-guided probabilistic roadmap planner with a neural surrogate model (PS-PRM). The planner explicitly incorporates the estimated quality of a perception task into motion planning for high-DoF robots. Our method uses a learned model to approximate perception scores and leverages GPU parallelism to enable efficient online replanning in dynamic settings. We demonstrate that our planner, evaluated on high-DoF robots, outperforms baseline methods in both static and dynamic environments in both simulation and real-robot experiments.
@misc{meng2025look, title = {Look as You Leap: Planning Simultaneous Motion and Perception for High-{DoF} Robots}, author = {Meng, Qingxi and Flores, Emiliano and Quintero-Peña, Carlos and Qian, Peizhu and Kingston, Zachary and Hamlin, Shannan K. and Unhelkar, Vaibhav and Kavraki, Lydia E.}, eprint = {2509.19610}, archiveprefix = {arXiv}, primaryclass = {cs.RO}, year = {2025}, note = {Under Review}, } - Constrained Nonlinear Kaczmarz Projection on Intersections of Manifolds for Coordinated Multi-Robot Mobile ManipulationIn IEEE International Conference on Robotics and Automation
Cooperative manipulation tasks impose various structure-, task-, and robot-specific constraints on mobile manipulators. However, current methods struggle to model and solve these myriad constraints simultaneously. We propose a twofold solution: first, we model constraints as a family of manifolds amenable to simultaneous solving. Second, we introduce the constrained nonlinear Kaczmarz (cNKZ) projection technique to produce constraint-satisfying solutions. Experiments show that cNKZ dramatically outperforms baseline approaches, which cannot find solutions at all. We integrate cNKZ with a sampling-based motion planning algorithm to generate complex, coordinated motions for 3 to 6 mobile manipulators (18–36 DoF), with cNKZ solving up to 80 nonlinear constraints simultaneously and achieving up to a 92% success rate in cluttered environments. We also demonstrate our approach on hardware using three Turtlebot3 Waffle Pi robots with OpenMANIPULATOR-X arms.
@inproceedings{agrawal2025cnkz, title = {Constrained Nonlinear {Kaczmarz} Projection on Intersections of Manifolds for Coordinated Multi-Robot Mobile Manipulation}, author = {Agrawal, Akshaya and Mayer, Parker and Kingston, Zachary and Hollinger, Geoffrey A.}, booktitle = {IEEE International Conference on Robotics and Automation}, pages = {7726--7732}, year = {2025}, doi = {10.1109/ICRA55743.2025.11127991}, }
2024
- arXiv
Efficient Multi-Robot Motion Planning for Manifold-Constrained Manipulators by Randomized Scheduling and Informed Path GenerationUnder ReviewMulti-robot motion planning for high degree-of-freedom manipulators in shared, constrained, and narrow spaces is a complex problem and essential for many scenarios such as construction, surgery, and more. Traditional coupled and decoupled methods either scale poorly or lack completeness, and hybrid methods that compose paths from individual robots together require the enumeration of many paths before they can find valid composite solutions. This paper introduces Scheduling to Avoid Collisions (StAC), a hybrid approach that more effectively composes paths from individual robots by scheduling (adding random stops and coordination motion along each path) and generates paths that are more likely to be feasible by using bidirectional feedback between the scheduler and motion planner for informed sampling. StAC uses 10 to 100 times fewer paths from the low-level planner than state-of-the-art baselines on challenging problems in manipulator cases.
@misc{guo2024stac, title = {Efficient Multi-Robot Motion Planning for Manifold-Constrained Manipulators by Randomized Scheduling and Informed Path Generation}, author = {Guo, Weihang and Kingston, Zachary and Hang, Kaiyu and Kavraki, Lydia E.}, eprint = {2412.00366}, archiveprefix = {arXiv}, primaryclass = {cs.RO}, year = {2024}, note = {Under Review}, }
2023
- Scaling Multimodal Planning: Using Experience and Informing Discrete SearchIEEE Transactions on Robotics
Robotic manipulation is inherently continuous, but typically has an underlying discrete structure, such as if an object is grasped. Many problems like these are multi-modal, such as pick-and-place tasks where every object grasp and placement is a mode. Multi-modal problems require finding a sequence of transitions between modes - for example, a particular sequence of object picks and placements. However, many multi-modal planners fail to scale when motion planning is difficult (e.g., in clutter) or the task has a long horizon (e.g., rearrangement). This work presents solutions for multi-modal scalability in both these areas. For motion planning, we present an experience-based planning framework ALEF which reuses experience from similar modes both online and from training data. For task satisfaction, we present a layered planning approach that uses a discrete lead to bias search towards useful mode transitions, informed by weights over mode transitions. Together, these contributions enable multi-modal planners to tackle complex manipulation tasks that were previously infeasible or inefficient, and provide significant improvements in scenes with high-dimensional robots.
@article{kingston2023tro, title = {Scaling Multimodal Planning: Using Experience and Informing Discrete Search}, author = {Kingston, Zachary and Kavraki, Lydia E.}, journal = {IEEE Transactions on Robotics}, volume = {39}, number = {1}, pages = {128--146}, year = {2023}, doi = {10.1109/TRO.2022.3197080}, }
2021
- Using Experience to Improve Constrained Planning on Foliations for Multi-Modal ProblemsIn IEEE/RSJ International Conference on Intelligent Robots and Systems
Many robotic manipulation problems are multi-modal—they consist of a discrete set of mode families (e.g., whether an object is grasped or placed) each with a continuum of parameters (e.g., where exactly an object is grasped). Core to these problems is solving single-mode motion plans, i.e., given a mode from a mode family (e.g., a specific grasp), find a feasible motion to transition to the next desired mode. Many planners for such problems have been proposed, but complex manipulation plans may require prohibitively long computation times due to the difficulty of solving these underlying single-mode problems. It has been shown that using experience from similar planning queries can significantly improve the efficiency of motion planning. However, even though modes from the same family are similar, they impose different constraints on the planning problem, and thus experience gained in one mode cannot be directly applied to another. We present a new experience-based framework, ALEF , for such multi-modal planning problems. ALEF learns using paths from single-mode problems from a mode family, and applies this experience to novel modes from the same family. We evaluate ALEF on a variety of challenging problems and show a significant improvement in the efficiency of sampling-based planners both in isolation and within a multi-modal manipulation planner.
@inproceedings{kingston2021, title = {Using Experience to Improve Constrained Planning on Foliations for Multi-Modal Problems}, author = {Kingston, Zachary and Chamzas, Constantinos and Kavraki, Lydia E.}, booktitle = {IEEE/RSJ International Conference on Intelligent Robots and Systems}, pages = {6922--6927}, year = {2021}, doi = {10.1109/IROS51168.2021.9636236}, }
2020
-
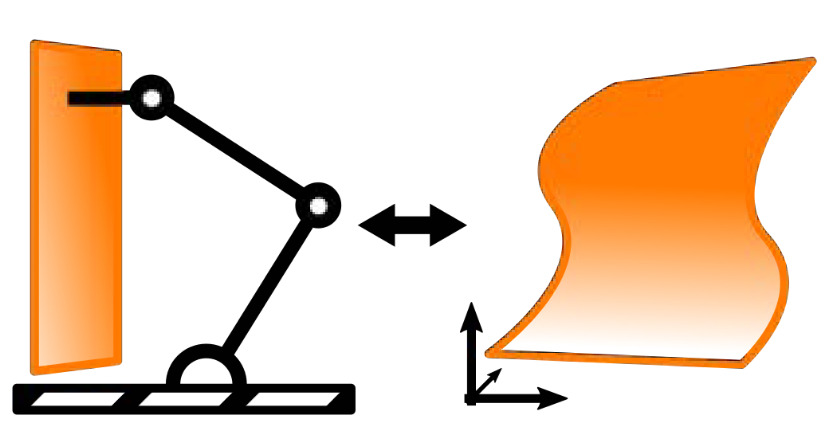Planning Under Manifold Constraints, Encyclopedia of Robotics@inbook{kingston2020book, title = {Encyclopedia of Robotics}, author = {Kingston, Zachary}, editor = {Ang, Marcelo H. and Khatib, Oussama and Siciliano, Bruno}, pages = {1--9}, year = {2020}, doi = {10.1007/978-3-642-41610-1_174-1}, isbn = {978-3-642-41610-1}, publisher = {Springer Berlin Heidelberg}, address = {Berlin, Heidelberg}, chapter = {Planning Under Manifold Constraints}, } - Informing Multi-Modal Planning with Synergistic Discrete LeadsIn IEEE International Conference on Robotics and Automation
Robotic manipulation problems are inherently continuous, but typically have underlying discrete structure, e.g., whether or not an object is grasped. This means many problems are multi-modal and in particular have a continuous infinity of modes. For example, in a pick-and-place manipulation domain, every grasp and placement of an object is a mode. Usually manipulation problems require the robot to transition into different modes, e.g., going from a mode with an object placed to another mode with the object grasped. To successfully find a manipulation plan, a planner must find a sequence of valid single-mode motions as well as valid transitions between these modes. Many manipulation planners have been proposed to solve tasks with multi-modal structure. However, these methods require mode-specific planners and fail to scale to very cluttered environments or to tasks that require long sequences of transitions. This paper presents a general layered planning approach to multi-modal planning that uses a discrete "lead" to bias search towards useful mode transitions. The difficulty of achieving specific mode transitions is captured online and used to bias search towards more promising sequences of modes. We demonstrate our planner on complex scenes and show that significant performance improvements are tied to both our discrete "lead" and our continuous representation.
@inproceedings{kingston2020leads, title = {Informing Multi-Modal Planning with Synergistic Discrete Leads}, author = {Kingston, Zachary and Wells, Andrew M. and Moll, Mark and Kavraki, Lydia E.}, booktitle = {IEEE International Conference on Robotics and Automation}, pages = {3199--3205}, year = {2020}, doi = {10.1109/ICRA40945.2020.9197545}, } - Decoupling Constraints from Sampling-Based PlannersIn Robotics Research
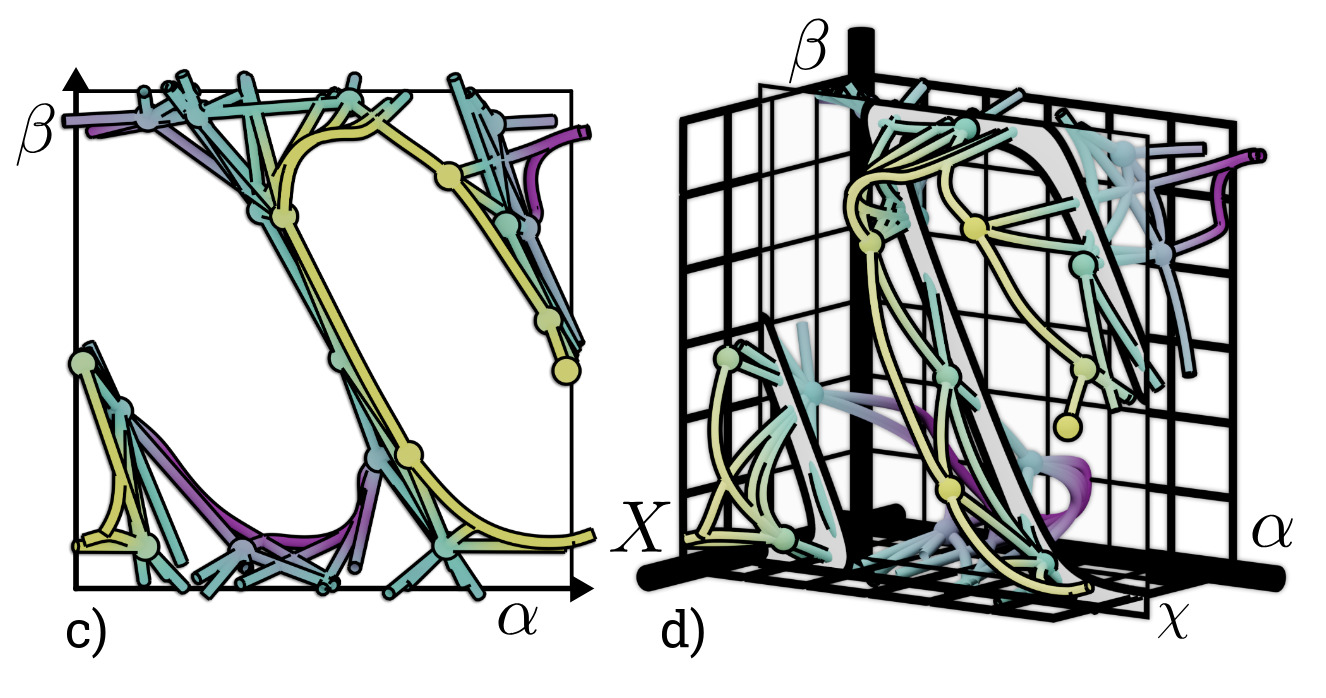
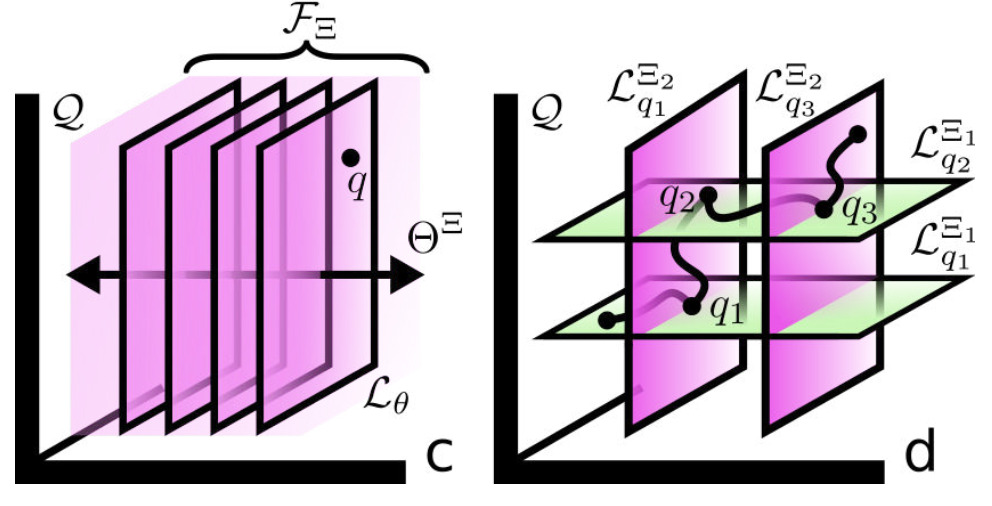
We present a general unifying framework for sampling-based motion planning under kinematic task constraints which enables a broad class of planners to compute plans that satisfy a given constraint function that encodes, e.g., loop closure, balance, and end-effector constraints. The framework decouples a planner’s method for exploration from constraint satisfaction by representing the implicit configuration space defined by a constraint function. We emulate three constraint satisfaction methodologies from the literature, and demonstrate the framework with a range of planners utilizing these constraint methodologies. Our results show that the appropriate choice of constrained satisfaction methodology depends on many factors, e.g., the dimension of the configuration space and implicit constraint manifold, and number of obstacles. Furthermore, we show that novel combinations of planners and constraint satisfaction methodologies can be more effective than previous approaches. The framework is also easily extended for novel planners and constraint spaces.
@incollection{kingston2020isrr, title = {Decoupling Constraints from Sampling-Based Planners}, author = {Kingston, Zachary and Moll, Mark and Kavraki, Lydia E.}, booktitle = {Robotics Research}, editor = {Amato, N. M. and Hager, G. and Thomas, S. and Torres-Torriti, M.}, pages = {913--928}, year = {2020}, doi = {10.1007/978-3-030-28619-4_62}, isbn = {978-3-030-28619-4}, publisher = {Springer International Publishing}, address = {Cham}, }
2019
- Exploring Implicit Spaces for Constrained Sampling-Based PlanningThe International Journal of Robotics Research
We present a review and reformulation of manifold constrained sampling-based motion planning within a unifying framework, IMACS (implicit manifold configuration space). IMACS enables a broad class of motion planners to plan in the presence of manifold constraints, decoupling the choice of motion planning algorithm and method for constraint adherence into orthogonal choices. We show that implicit configuration spaces defined by constraints can be presented to sampling-based planners by addressing two key fundamental primitives, sampling and local planning, and that IMACS preserves theoretical properties of probabilistic completeness and asymptotic optimality through these primitives. Within IMACS, we implement projection- and continuation-based methods for constraint adherence, and demonstrate the framework on a range of planners with both methods in simulated and realistic scenarios. Our results show that the choice of method for constraint adherence depends on many factors and that novel combinations of planners and methods of constraint adherence can be more effective than previous approaches. Our implementation of IMACS is open source within the Open Motion Planning Library and is easily extended for novel planners and constraint spaces.
@article{kingston2019imacs, title = {Exploring Implicit Spaces for Constrained Sampling-Based Planning}, author = {Kingston, Zachary and Moll, Mark and Kavraki, Lydia E.}, journal = {The International Journal of Robotics Research}, volume = {38}, number = {10--11}, pages = {1151--1178}, month = sep, year = {2019}, doi = {10.1177/0278364919868530}, }
2018
- Sampling-Based Methods for Motion Planning with ConstraintsAnnual Review of Control, Robotics, and Autonomous Systems
Robots with many degrees of freedom (e.g., humanoid robots and mobile manipulators) have increasingly been employed to accomplish realistic tasks in domains such as disaster relief, spacecraft logistics, and home caretaking. Finding feasible motions for these robots autonomously is essential for their operation. Sampling-based motion planning algorithms have been shown to be effective for these high-dimensional systems. However, incorporating task constraints (e.g., keeping a cup level, writing on a board) into the planning process introduces significant challenges. is survey describes the families of methods for sampling-based planning with constraints and places them on a spectrum delineated by their complexity. Constrained sampling-based methods are based upon two core primitive operations: (1) sampling constraint-satisfying configurations and (2) generating constraint-satisfying continuous motion. Although the basics of sampling-based planning are presented for contextual background, the survey focuses on the representation of constraints and sampling-based planners that incorporate constraints.
@article{kingston2018ar, title = {Sampling-Based Methods for Motion Planning with Constraints}, author = {Kingston, Zachary and Moll, Mark and Kavraki, Lydia E.}, journal = {Annual Review of Control, Robotics, and Autonomous Systems}, volume = {1}, number = {1}, pages = {159--185}, year = {2018}, doi = {10.1146/annurev-control-060117-105226}, }
2017
-
Robonaut 2 and You: Specifying and Executing Complex OperationsIn IEEE Workshop on Advanced Robotics and its Social ImpactsCrew time is a precious resource due to the expense of trained human operators in space. Efficient caretaker robots could lessen the manual labor load required by frequent vehicular and life support maintenance tasks, freeing astronaut time for scientific mission objectives. Humanoid robots can fluidly exist alongside human counterparts due to their form, but they are complex and high-dimensional platforms. This paper describes a system that human operators can use to maneuver Robonaut 2 (R2), a dexterous humanoid robot developed by NASA to research co-robotic applications. The system includes a specification of constraints used to describe operations, and the supporting planning framework that solves constrained problems on R2 at interactive speeds. The paper is developed in reference to an illustrative, typical example of an operation R2 performs to highlight the challenges inherent to the problems R2 must face. Finally, the interface and planner is validated through a case-study using the guiding example on the physical robot in a simulated microgravity environment. This work reveals the complexity of employing humanoid caretaker robots and suggest solutions that are broadly applicable.
@inproceedings{baker2017r2, title = {Robonaut 2 and You: Specifying and Executing Complex Operations}, author = {Baker, William and Kingston, Zachary and Moll, Mark and Badger, Julia and Kavraki, Lydia E.}, booktitle = {IEEE Workshop on Advanced Robotics and its Social Impacts}, pages = {1--8}, month = mar, year = {2017}, doi = {10.1109/ARSO.2017.8025204}, address = {Austin, TX}, }
2015
- Humanoids
Kinematically Constrained Workspace Control via Linear OptimizationIn IEEE-RAS International Conference on Humanoid RobotsWe present a method for Cartesian workspace control of a robot manipulator that enforces joint-level acceleration, velocity, and position constraints using linear optimization. This method is robust to kinematic singularities. On redundant manipulators, we avoid poor configurations near joint limits by including a maximum permissible velocity term to center each joint within its limits. Compared to the baseline Jacobian damped least-squares method of workspace control, this new approach honors kinematic limits, ensuring physically realizable control inputs and providing smoother motion of the robot. We demonstrate our method on simulated redundant and non-redundant manipulators and implement it on the physical 7-degree-of-freedom Baxter manipulator. We provide our control software under a permissive license.
@inproceedings{kingston2015lc3, title = {Kinematically Constrained Workspace Control via Linear Optimization}, author = {Kingston, Zachary and Dantam, Neil T. and Kavraki, Lydia E.}, booktitle = {IEEE-RAS International Conference on Humanoid Robots}, pages = {758--764}, month = nov, year = {2015}, doi = {10.1109/HUMANOIDS.2015.7363455}, }
